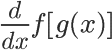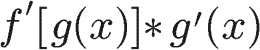Derivative Rules
What are derivative rules?
Derivative rules are used when the standard formula may not be applicable.
Say we have two functions f(x) and g(x). In certain situations, we have to follow specific strategies to find the derivative, which are called derivative rules. Below is each rule and how they are applied to different situations you will encounter.
Sum Rule
You've likely already used the sum rule without realizing it! It applies to functions with several appearances of a variable.
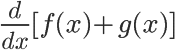

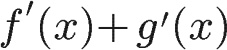
Difference Rule
Like the sum rule, you've likely already used the difference rule! It's the same as the sum rule, but with subtraction.
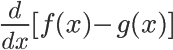

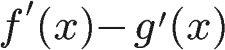
Quotient Rule
The quotient rule has a very unique behavior:
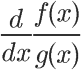

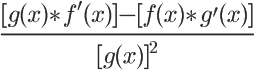
This one looks intimidating, I know! When I took calculus, my teacher taught us a pnemonic device to help remember the quotient rule. It doesn't make much sense out of context, but for some reason, it's' easy to remember.
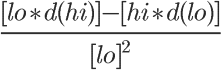
To translate this into something that makes sense, "lo" would be the denominator g(x), "d" means to take the derivative, and "hi" is the numerator f(x). Say this in your head as "low dee high minus high dee low over low squared". So you take the lower function, multiply it by the derivative of the higher function, subtract the higher function multiplied by the derivative of the lower function, and then divide all of that by the square of the lower function.
Product Rule
The product rule also has its own unique behavior, but is a bit simpler than the quotient rule. It might look hard to remember, but it's just multiplying the first function by the second function's derivative, then adding the second function multiplied by the first function's derivative.
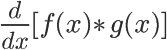

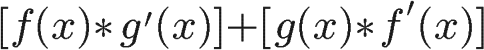
Chain Rule
The chain rule is used when you have one function nested inside of another function. It generally helps to derive the nested function first.